The first constraint tells us that's what y is So negative 5x plus 8 is equal to negative 2 Now, we have one equation with one unknown We can just solve for x We have 10x plus So we can multiply it We can distribute this 2 onto both of these terms So we have 2 times negative 5x is negative 10x And then 2 times 8 is 161) is a critical point The second derivative test f xx = 2;f yy = 2;f xy = 0 shows this a local minimum withY is the set of even numbers X \Y is the set of all even numbers in the interval ( 2;4), ie X \Y = f0;2g X Y = fx 2R j 2 < x < 4 or x = 2k for some k 2Zg (f) Let A be the xzplane in R3 and B be the yzplane in R3 Use set comprehension notation to describe the sets A\B and AB Answer A = 8 < 2 4 x y z 3 5 2R3
Buad 306 Chapter 3 Forecasting Everyday Forecasting Weather
X y/2-x-y/3=8 x y/3 x-y/4=11
X y/2-x-y/3=8 x y/3 x-y/4=11- y'= 16/3 Implicit differentiation of the given equation, term by term gives 10x 3xy' y=0 For getting y'(3), put x=3 and for y put 17, because it is given that y(3)=17 Accordingly, 10(3) 3 3y' 17 =0 3y'= 16 y'= 16/34 0 0 6 1 1 8 2 2 3 Figure 1412 f(x,y) = x2 y2 (AP) As in this example, the points (x,y) such that f(x,y) = k usually form a curve, called a level curve of the function A graph of some level curves can give a good idea of the shape of the surface;



2
With initial values y 0 and y 0 is (123) y x y 0 cosx y 0 sinx Example 122 Solve y y 0 with given initial values y 0 y 0 Now ex and e x are solutions of this differential equation, so the general solution is a linear combination of these But we won't have as easy a time finding a solution like (123), since these functions do3x – y = 5 ii x – 2y = 1 ;Example 5 X and Y are jointly continuous with joint pdf f(x,y) = (e−(xy) if 0 ≤ x, 0 ≤ y 0, otherwise Let Z = X/Y Find the pdf of Z The first thing we do is draw a picture of the support set (which in this case is the first
Subject to the constraint 2x2 (y 1)2 18 Solution We check for the critical points in the interior f x = 2x;f y = 2(y1) =)(0;To find the xintercept (s), substitute in 0 0 for y y and solve for x x Solve the equation Tap for more steps Rewrite the equation as x 2 − 8 = 0 x 2 8 = 0 Add 8 8 to both sides of the equation Take the square root of both sides of the equation to eliminate the exponent on the left sideViết biểu thức x 36 x 2 y 12 x y 28 y 3 dưới dạng lập phương của một hiệu Trả lời (1) Xem đáp án »
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange x^2y^2=8 xy=2 Using the second thing, we can add y to both sides and subtract 2 from both sidesthis gives y = x 2 and substituting this into the first equation, we haveSolution (a) Since cos2 sin2 = 1, we get (x=4)2 (y=5)2 = 1, ie, x2 16 y2 25 = 1 which is an ellipse with the xintercepts x = 4, the yintercepts y = 5 But since ˇ=2 ˇ=2, we have 0 cos 1 so the graph consists of only the portion



What Is The Value Of X Y If 7432x64y Is Divisible By Both 8 As Well As 9 X And Y Being Single Digit Number Quora
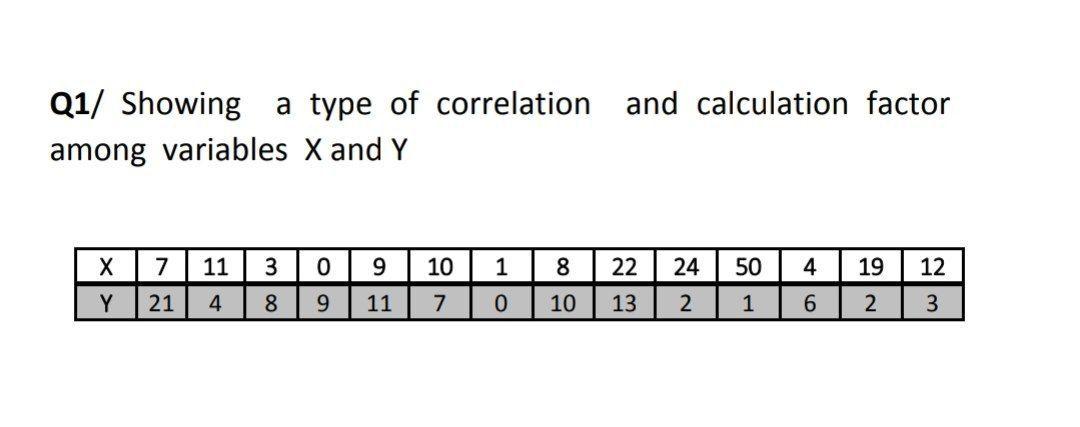



Solved And Calculation Factor Q1 Showing A Type Of Chegg Com
We get their width by subtracting the xcoordinate of the edge on the left curve from the xcoordinate of the edge on the right curve (If you get mixed up and subtract the right from the left you'll27 Answers Macpin Julaton Answered 4 years ago Given 3xy=12, find 8^x/2^y 8^x = (2^3)^x Hence, 8^x = 2^ (3x) because of law of exponent product rule Hence, we have (2^ (3x))/ (2^y) Hence, we have 2^ (3xy) because of law of exponent quotient rule Since 3xy=12, we have 2^12It looks much like a topographic map of the surface In figure 1412




X Y 2 X Y 3 8 Y X Y 3 X Y 4 11 Brainly Lat




Worked Example Implicit Differentiation Video Khan Academy
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Math Input NEW Use textbook math notation to enter your math Try itSolve for y y Tap for more steps Rewrite the equation as 8 ( y 2) = ( x 3) 2 8 ( y 2) = ( x − 3) 2 8 ( y 2) = ( x 3) 2 8 ( y 2) = ( x − 3) 2 Divide each term by 8 8 and simplify Tap for more steps Divide each term in 8 ( y 2) = ( x 3) 2 8 ( y 2) = ( x − 3) 2 by 8 8



2



2
Simple and best practice solution for y=2(x3)(x4) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itFirst type the equation 2x3=15 Then type the @ symbol Then type x=6 Try it now 2x3=15 @ x=6 Clickable Demo Try entering 2x3=15 @ x=6 into the text box After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer is right More ExamplesExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music



Solved 1 A Combinational Circuit Is Defined By The Following Three Boolean Functions F1 X Y Z Xy F2 X Yz Xz F3 Xy Z X Y Design And Course Hero



3 8 Implicit Differentiation Calculus Volume 1
2x – 3y = 7 asked in Linear Equations in Two Variables by Aryan01 ( 502k Sketch the area between two curves and then find the area This is using summations y=2x 1/3, y= (1/8)x 2, 0The given equations are `(x y 8)/2 = (x 2y 14)/3 = (3x y 12)/11` ie,`( xy−)/2 = (3xy−12)/11` By cross multiplication, we get
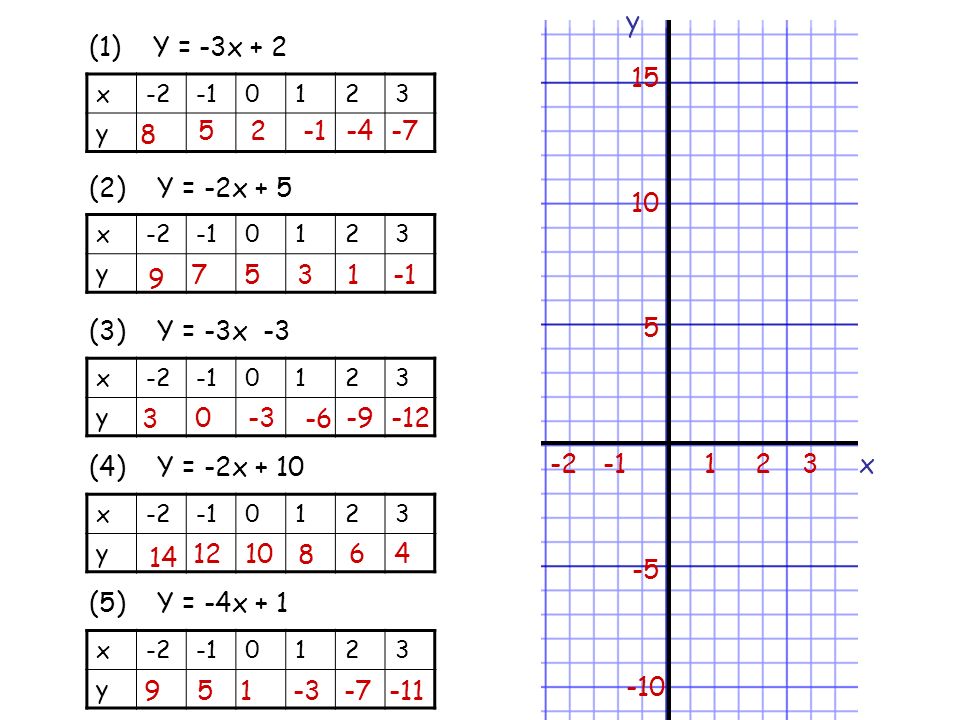



Drawing Linear Graphs Starter Multiplying Negative Numbers 1 3 X 4 4 7 6 X 10 3 X 3 9 13 7 X 16 4 X Ppt Download




Solving A System Of Equations Using A Matrix Precalculus Socratic
Y = 8 x^2, y = x^2, x = 3, x = 3Sketch the region enclosed by the given curves Decidewhether to integrate with respect to x or y Draw a typical approximSignals and Systems Part 11/ Solutions S313 We see that the system is timeinvariant from T 2T 1x(t T) = T 2y (t T)l = y 2(t T), Tx(t T) = y 2(t T) (b) False Two nonlinear systems in cascade can be linear, as shown in Figure S310 Ex 25, 9Verify (i) x3 y3 = (x y) (x2 – xy y2)LHS x3 y3We know (x y)3 = x3 y3 3xy (x y)So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xy




11 If X Y 8 And Xy 3 Find The Values Of Ii 3 X2 Y2 1 X Y Iii 5 X2 Y2 4 X Y 11 2



X Y 2 X Y 3 8 X Y 3 X Y 4 11 Gauthmath
Click here👆to get an answer to your question ️ Solve by matrix method 2x 3y 3z = 5 x 2y z = 4 3x y 2z = 3Answer (1 of 8) Let k = 2^x = 3^y = 6^{z} x = \frac{\ln k}{\ln 2} y = \frac{\ln k}{\ln 3} z = \frac{\ln k}{\ln 6} \begin{align*} \frac{1}{x} \frac{1}{y} \frac(x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6 (x y z) 2 = x 2 y 2 z 2 2xy 2xz 2yz




Answers
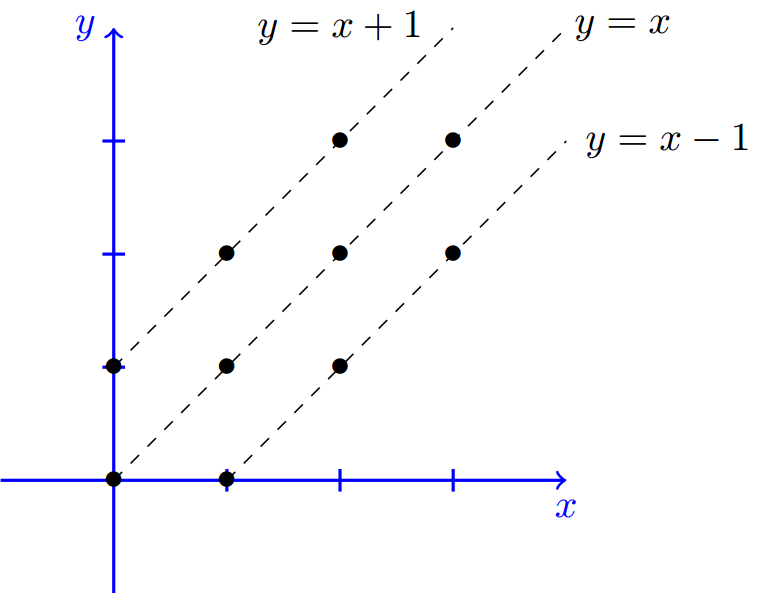



Solved Problems Marginal Pmf Independence Two Random Variables
Theorem 36 Let F be any partition of the set S Define a relation on S by x R y iff there is a set in F which contains both x and y Then R is an equivalence relation and the equivalence classes of R are the sets of F Pf Since F is a partition, for each x in S there is one (and only one) set of F which contains xX 2/3 = 4 , ( x 2/3) 3 = 4 3, x 2 = 64 , or If x=8 , then y=8 , and the tangent line passing through the point (8, 8) has slope 1 If x=8 , then y=8 , and the tangent line passing through the point (8, 8) has slope 1 Click HERE to return to the list of problems SOLUTION 15 Since the equation x 2 xy y 2 = 3 represents an ellipse, the largest and smallest values of y will occur at theChoose one of the equations and solve it for x by isolating x on the left hand side of the equal sign 3x2y=22 3 x 2 y = 2 2 Subtract 2y from both sides of the equation Subtract 2 y from both sides of the equation 3x=2y22 3 x = − 2 y 2 2 Divide both sides by 3 Divide both sides by 3




X Y 2 X Y 3 8 Amp X Y 3 X Y 4 11 Method Of Elimination How To Solve Brainly In




Curve Fitting And Solution Of Equation
Simple and best practice solution for Y3=8(x2) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, soLinearequationcalculator y=x en Related Symbolab blog posts Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series Over the next few weeks, we'll be showing how Symbolab Example 11 Important Example 12 Example 13 v = 3 is the solution But we have to find x & y u = 𝟏/𝒙 2 = 1/𝑥 x = 𝟏/𝟐 v = 𝟏/𝒚 3 = 1/𝑦 y = 𝟏/𝟑 Hence, x = 1/2 , y = 1/3 is the solution of the given equation Show More




Solving A System Of Equations Using A Matrix Precalculus Socratic



2
16−x 2) = 2x2 3(16−x2)−4x−5 = −x −4x43 g0(x) = 0 ⇒ −2x−4 = 0 ⇒ x = −2 y 2= 16−x = 16−4 = 12 ⇒ y = ±2 √ 3 Now f(1,0) = −7 and f(−2,±2 √ 3) = 47 Thus the maximum value of f(x,y) on the disc x 2y ≤ 16 is f(−2,±2 √ 3) = 47, and the minimum value is f(1,0) = −7Y = lnx,1 ≤ x ≤ 3 about the xaxis Solution This one's easy (since we don't have to evaluate the integral!) y0 = 1 x, so A = Z 3 1 2πlnx r 1 1 x2 dx Problem 3 Set up, but do not evaluate, an integral for the area of the surface obtained by rotating y = secx,0 ≤ x ≤ π/4 about the yaxis Solution First, note that y0 2x y = 5 ;



2



2
SOLUTION 11 Begin with x 2 (yx) 3 = 9 If x=1 , then (1) 2 ( y1 ) 3 = 9 so that ( y1 ) 3 = 8 , y1 = 2 , y = 3 , and the tangent line passes through the point (1, 3) Now differentiate both sides of the original equation, getting D ( x 2 (yx) 3) = D ( 9 ) , D ( x 2) D (yx) 3 = D ( 9 ) , 2x 3 (yx) 2 D (yx) = 0 , 2x 3 (yx) 2 (y'1) = 0 , Answered Author has 29 answers Step 1 To find d 2 y d x 2 of 2 x 2 y 2 = 4 Step 2 2 x 2 y 2 = 4 On differentiating with respect to x we get 4 x 2 y d y d x = 0X^3 x^2 y x y^2 y^3 Natural Language;




Solved Given Are Five Observations For Two Variables X And Chegg Com




If X Y 2 3 Y Z 4 7 Then Find X Y Z Youtube
(4,2) dy Figure 3 The 2area between x = y and y = x − 2 and one horizontal rectangle The height of these rectangles is dy;2x – y = 7 iii x y = 11 ; Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2 Always expand each term in the bracket by all the other terms in the other brackets, but never multiply two or




X Y 2 X Y 3 8 X Y 3 X Y 4 11 Brainly In



2
Determine whether y varies directly with x, If so, find the constant of variation k and write the equation x y 4 64 7 112 10 16 13 8 Would like for someone to explain if possible1 y =2x 2 x =2y 3 x2 y2 =8 Notice that if one variable is zero, then the other is as well This violates equation (3), so we don't need to consider it Let's substitute (1) into (2) x =42x =) = ± 1 2 Plugging this value into equations (1) and (2) give us the following equation y = ±x We can then plug this into equation (3) Then 2 x2Describe this intersection geometrically ⇒



2




If X Y 3 X Y 2 Then What Is The Value Of X 3 Y 3 A 6 B 7 C 8 D 9 E None Of These
Answer No (332) Solve the system of equations Problem 3 2 x − y = − 5 y = 1 − 3 x \displaystyle \begin {array} {l} 2x y = 5 \\ y = 13x \end {array} 2x−y = −5 y = 1 −3x Answer x = 1, y = 2 Problem 4 3 x − y = 1 3 3 y − 2 x = − 4( x y ) 2 = x 2 2xy y 2 and ( x y ) 2 = x 2 2xy y 2 Rewrite the above equation, we have ( x y ) 2 = x 2 y 2 2xy 4xy = ( x y ) 2 4xy (1) Given that `"x y" = 7/2 "and xy" =5/2` Substitute the values of ( x y ) and (xy) in equation (1), we have ( x y ) 2 =` (7/2)^2 4(5/2)` = `49/4 10 = 9/4` ⇒ x y = ` sqrt(2,4,5) y z x 4 2 5 Note that if you imagine looking down from above, along the z axis, the positive z axis (4,2,5) ⇒ 11 Find an equation of the sphere with center at (2,1,−1) and radius 4 Find an equation for the intersection of this sphere with the yz plane;




Solved Find The First Partial Derivatives Of The Function Chegg Com
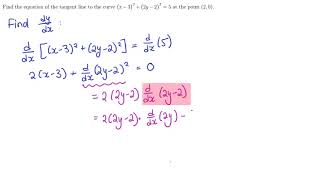



Implicit And Logarithmic Differentiation
X^3 y^3 z^3 3x^2y 3xy^2 3x^2z 3z^2x 3y^2z 3z^2y 6xyz Lennox Obuong Algebra Student Email obuong3@aolcomSubtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0 Reorder the terms Reorder the terms This is true for any x This is true for any x Use the distributive property to multiply xy by x^ {2}xyy^ {2 Solve for x,y (xy8)/2= (x2y14)/3 = (3xy12)/11 (class 10 CBSE SAMPLE PAPER 1718 MATHS) Get the answers you need, now!
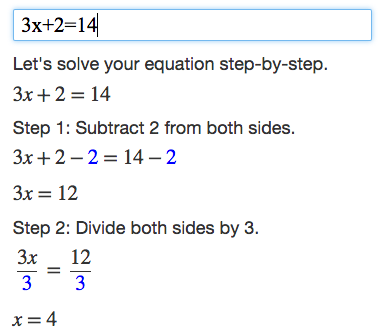



Algebra Calculator Tutorial Mathpapa



Multiple Representations Of Relations Worksheet
X is the interval ( 2;4);



Algebra Calculator Tutorial Mathpapa



2



Solve For X And Y 1 3x Y 1 3x Y 3 4 1 2 3x Y 1 2 3x Y 1 8 Sarthaks Econnect Largest Online Education Community



2




Find The Value Of X Y And Z From The Following Equation I Ii Iii X Y Z X Z Y Z 9 5 7




Find Slope Of Tangent Line To Curve 2xy Y 3 4 At 3 2 Youtube



2




Buad 306 Chapter 3 Forecasting Everyday Forecasting Weather




X Y 2 X Y 3 8 Amp X Y 3 X Y 4 11 Method Of Elimination How To Solve Brainly In




X Y 2 X Y 3 8 And X Y 3 X Y 4 11 Maths Pair Of Linear Equations In Two Variables Meritnation Com




Ex 3 2 7 I Class 12 Matrices Find X And Y If X Y And X




Pdf Nique Dietary Patterns And Chronic Disease Isk Profiles Of Adult Men The Framingham Utrition Studies Semantic Scholar




Tarea Correlacion



How To Solve The Equations For X Y 8 X Z 13 Z W 6 And W Y 8 Quora
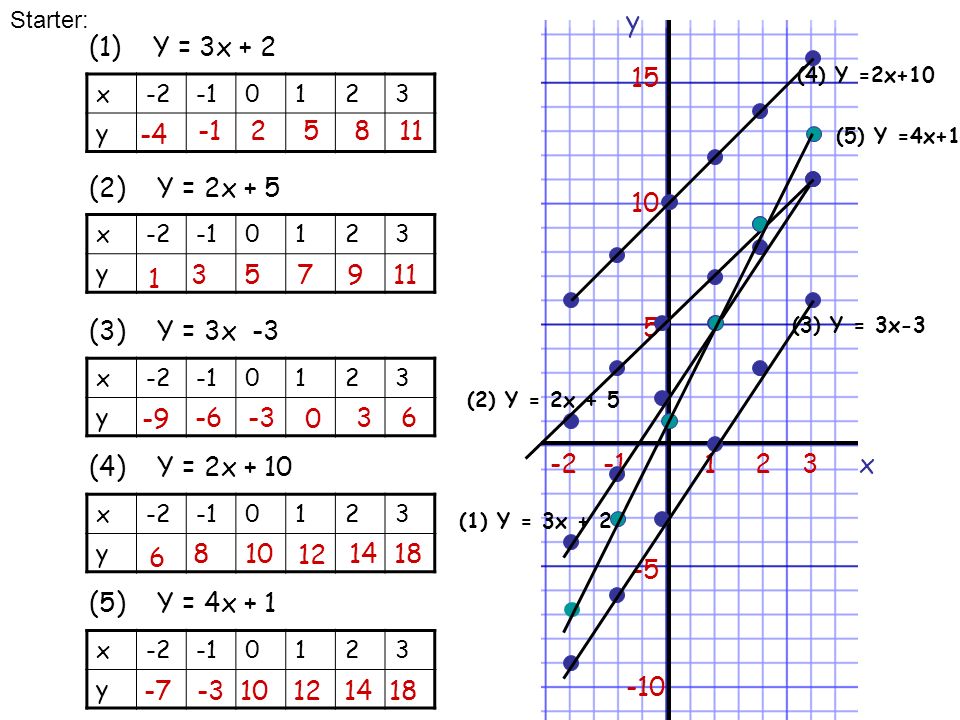



Drawing Linear Graphs Starter Multiplying Negative Numbers 1 3 X 4 4 7 6 X 10 3 X 3 9 13 7 X 16 4 X Ppt Download




X Y 2 X Y 3 8 Amp X Y 3 X Y 4 11 Method Of Elimination How To Solve Brainly In



2




Ex 3 2 7 I Class 12 Matrices Find X And Y If X Y And X
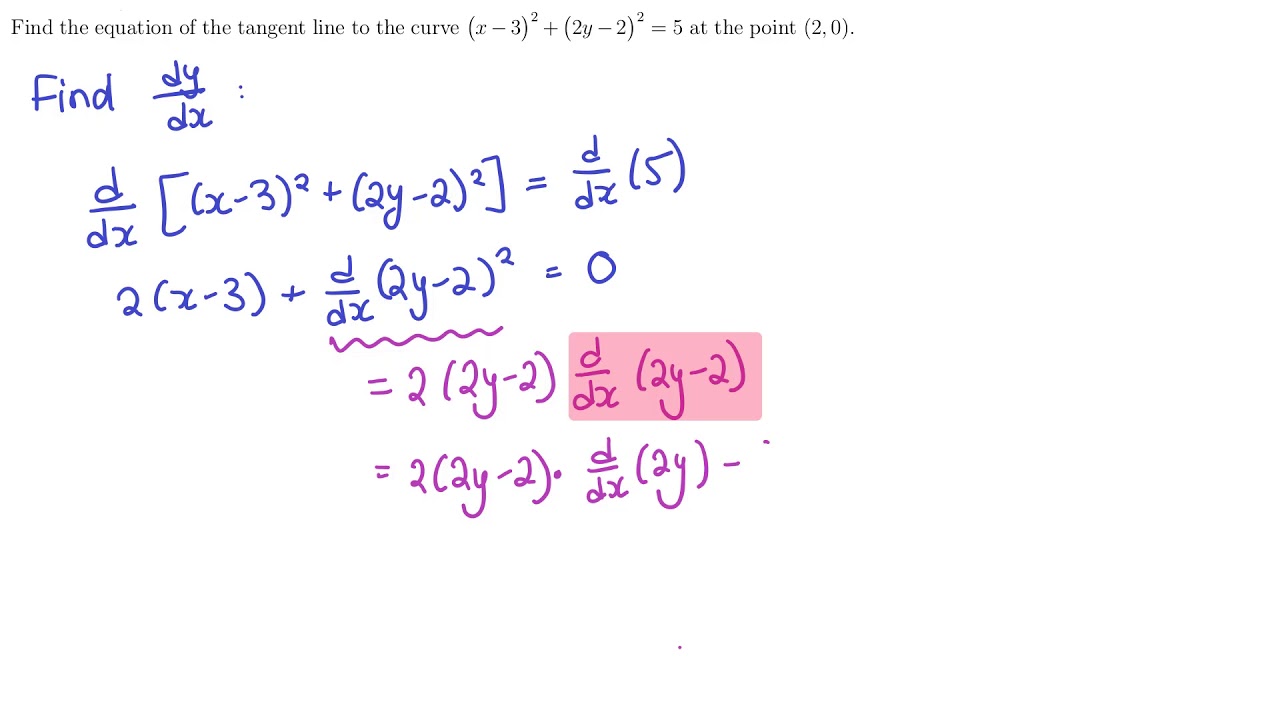



Implicit And Logarithmic Differentiation




Example 30 Find Coordinates Of Point Where Line Through A 3 4 1



2




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf



2




X Y 2 X Y 3 8 X Y 3
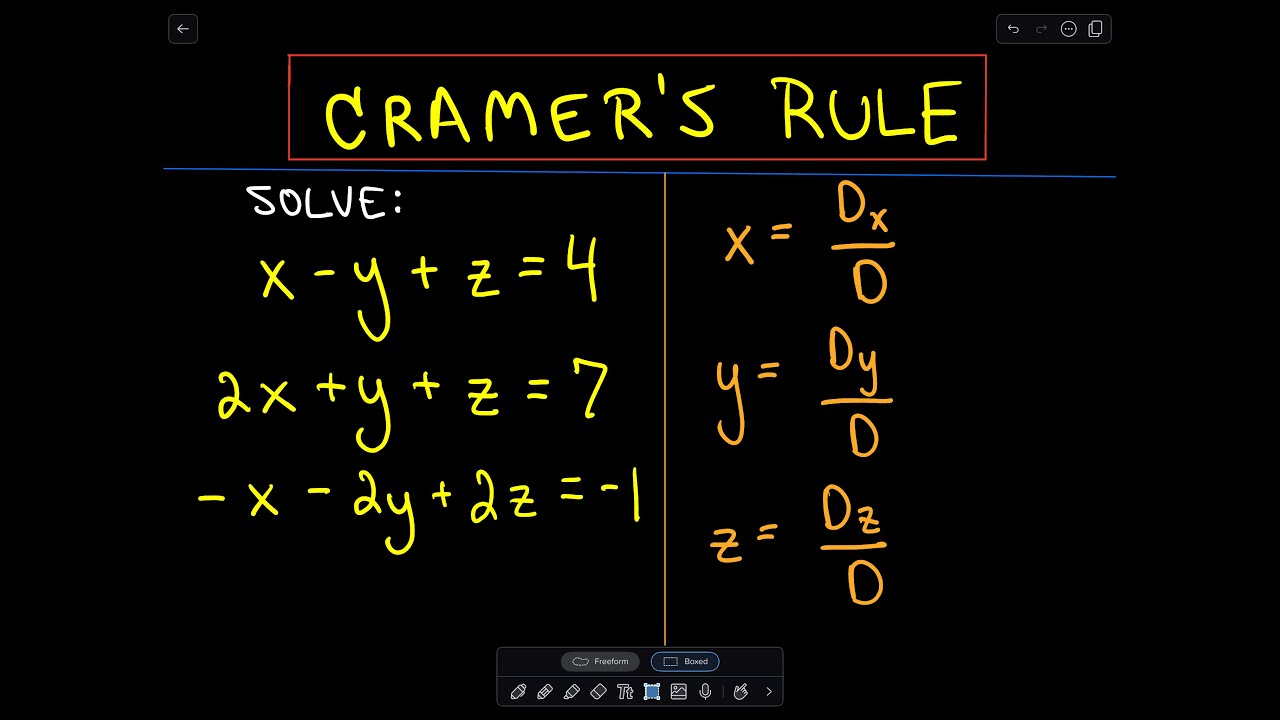



Cramer S Rule To Solve A System Of 3 Linear Equations Example 2 Youtube




Solucionario Del Algebra Baldor Ejercicios Resueltos



2




Solve For X Y X Y 8 2 X 2y 14 3 3x Y 12 11 Class 10 Cbse Sample Paper 17 18 Maths Brainly In



2




Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy



2




Graph Graph Inequalities With Step By Step Math Problem Solver




Solved Haverty S Furniture Is A Family Business That Has Been Selling To Retail Points Customers In The Chicago Area For Many Years The Company Advertises Extensively On Radio Tv And The Internet Emphasizing



Systems Of Linear Equations




Geometry Common Core Style Parcc Practice Test Question 5 Day 150



3 8 Implicit Differentiation Calculus Volume 1



2




Solving A System Of Equations Using A Matrix Precalculus Socratic




Linear Equations Questions And Answers Topperlearning




X 3 Y 4 11 5x 6 Y 3 7 Solve In Substitution Method Brainly In




X Y 2 X Y 3 8 X Y 3 X Y 4 4




Let A 1 2 3 14 Define A Relation R From A To A By R X Y 3x Y 0 Where X Y A Write Down Its Domain Co Domain And Range




If 2x 3y 12 And Xy 6 Find The Value Of 8x 3 27y 3




X Y 2 X Y 3 8 And X Y 3 X Y 4 11 Maths Pair Of Linear Equations In Two Variables Meritnation Com




Video Ebook Given Are Five Observations For Two Variables Z And Y Use Table 2 Of Appendix B 3 4 5 8 6 11 4 14 Ro Homeworklib




Q 1 Implement The Following Boolean Functions Using Decoders I F1 X Y Z X Z Homeworklib



2




Solve The Equations For X A N D Y 3 X 9 Xx 3 Y 8 Xx 2 Y 4 X



2




Find Slope Of Tangent Line To Curve 2xy Y 3 4 At 3 2 Youtube




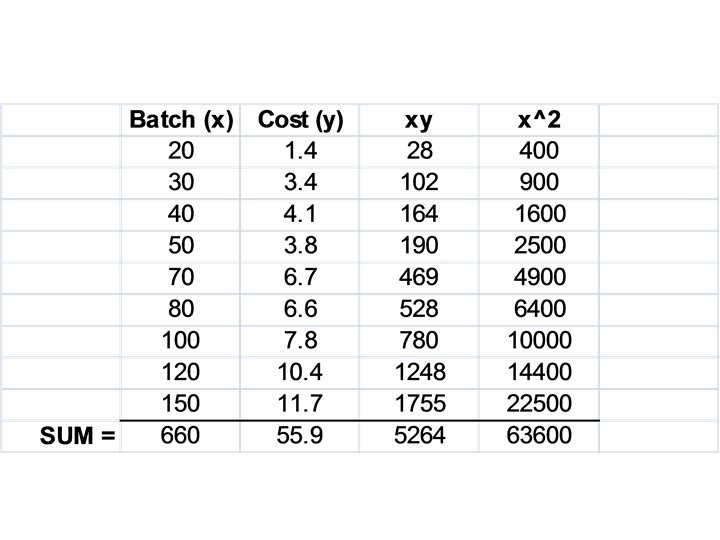
Solved 4 8 Pts Given The Following Table Subject X Y 10 Chegg Com
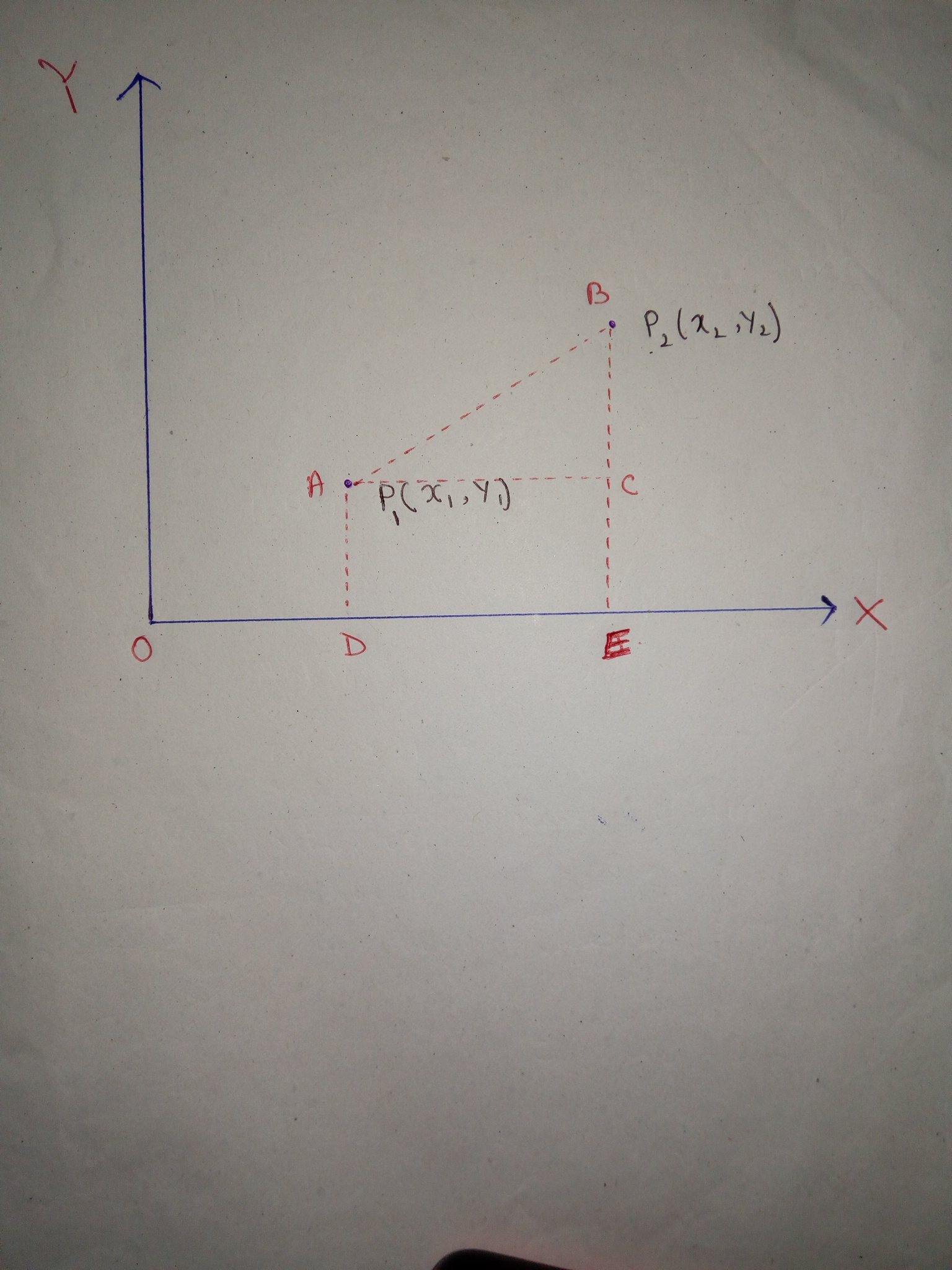



Distance Formula Algebra Socratic




Example 30 Find Coordinates Of Point Where Line Through A 3 4 1




Solutions Manual For Beginning Algebra 7th Edition By Martin Gay By Cndps109 Issuu




Curve Fitting And Solution Of Equation




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3



2




If X Y X Y 4 1 T H E N X 2 Y 2 X 2 Y 2 8 17 B 17 8 C 16 1 D 25 9



2



If 2 3 8 3 7 27 4 5 32 5 8 60 6 7 72 Then The Value Of 7 8 Is Quora




Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6




11 If X Y 8 And Xy 3 Find The Values Of Ii 3 X2



Graph Graph Inequalities With Step By Step Math Problem Solver




Example 30 Find Coordinates Of Point Where Line Through A 3 4 1




2 6 X Y 2 X Y 3 8 X Y 3 X Y 4 4
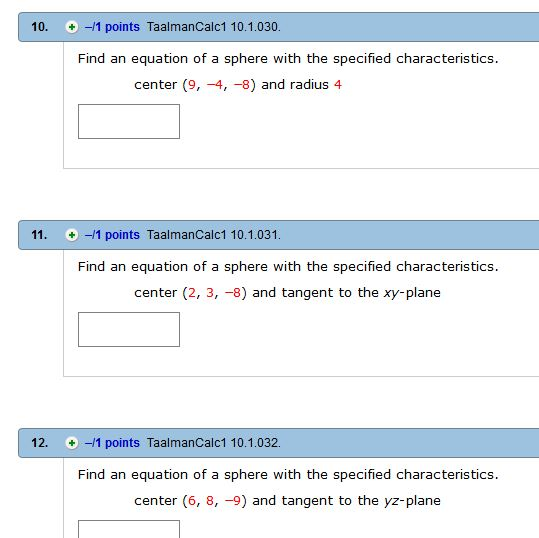



Solved 10 11 Points Taalmancalc1 10 1 030 Find An Chegg Com



2




Example 28 Solve By Matrix Method 3x 2y 3z 8 2x Y Z 1 Examples




Solved For The Following Data X Y 3 3 6 9 5 8 4 3 10 7 5 9 Chegg Com




Implicit And Logarithmic Differentiation



0 件のコメント:
コメントを投稿